Типовые задачи >  Системы линейных уравнений >  Методы решения

Решение систем линейных алгебраических уравнений

Способы решения систем линейных алгебраических уравнений в основном разделяются на две группы:

• точные методы, представляющие собой конечные алгоритмы вычисления корней (матричный метод, правило Крамера, метод Гаусса и др.);
• итерационные методы, позволяющие получать корни с заданной точностью путем сходящихся процессов.

Пусть дана система из n линейных уравнений с n неизвестными:

(1)

Обратите внимание, что в стандартной форме система линейных уравнений слева содержит слагаемые, содержащие только неизвестные величины, причем порядок следования аргументов в каждом уравнении должен быть строго одинаковым.

Совокупность чисел 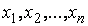(вектор x), обращающих систему (1) в тождество, называется решением этой системы, а сами числа 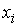– ее корнями.

Матричный метод. Если обозначить через A матрицу коэффициентов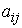

,

через b – вектор-столбец свободных членов, x – вектор-столбец решений, то в общем виде решение системы в матричной форме

x = A^–1b,

где A^–1 – обратная матрица матрице A. Это решение возможно при условии, что определитель матрицы A не равен нулю, т.е. detA = Δ ≠ 0.

Таким образом, для решения системы необходимо вычислить обратную матрицу A^–1 и умножить ее слева на столбец свободных членов.

Правило Крамера. Формулы Крамера для вычисления корней системы линейных алгебраических уравнений не требуют обращения матрицы A, а используют основной Δ и вспомогательные Δ₁,Δ₂, ..., Δ_n определители системы:

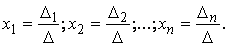
Здесь вспомогательный определитель Δ_j – это определитель матрицы коэффициентов, в которой j-й столбец заменен столбцом свободных членов, например

Для вычисления корней по формуле Крамера требуется иметь процедуры для расчета определителя матрицы, так как трудоемкость ручного расчета при n > 4 весьма велика.

Одним из наиболее простых методов вычисления определителя является алгоритм, в основе которого лежит приведение путем элементарных преобразований исходной матрицы A к треугольному виду A_Δ (все элементы выше или ниже главной диагонали равны нулю). Для преобразованной треугольной матрицы определитель пропорционален произведению элементов главной диагонали. Знак определителя матрицы A зависит от числа перестановок строк l и столбцов s при преобразовании к треугольной матрице

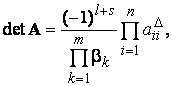
где a_ij^Δ – элементы главной диагонали преобразованной матрицы; β_k– множители, использованные при преобразовании матрицы.

Пример вычисления определителя

Метод Гаусса. Наиболее часто используемым приемом решения систем линейных алгебраических уравнений является алгоритм последовательного исключения неизвестных, называемый методом Гаусса. Метод заключается в преобразовании исходной системы

(2)

к эквивалентной, имеющей треугольную матрицу коэффициентов

(3)

В преобразованной системе 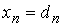, а остальные корни находятся на "обратном" проходе:

Преобразование исходной системы (1.2) к системе с треугольной матрицей коэффициентов (1.3) можно осуществить, например, следующим образом. Если a₁₁ ≠ 0, то поделим первое уравнение на a₁₁:

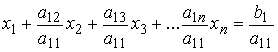
Затем из каждого последующего уравнения вычтем первое, умноженное на коэффициент при x₁, тогда из системы всех этих уравнений исключим x₁. Эту же процедуру повторим для системы уравнений 2...n, из которых исключена переменная x₁, исключая из 3...n уравнений аргумент x₂ и т.д.

Пример использования метода

Отметим, что диагональный элемент треугольной матрицы системы (1.3) не может быть равен нулю, так как в этом случае определитель матрицы также равен нулю. Кроме того, рекомендуют начинать алгоритм исключения переменных с перестановки уравнений таким образом, чтобы диагональный элемент, соответствующий номеру исключаемой переменной, был не только ненулевым, но и максимальным по модулю.

Итак, выше рассмотрены матричный метод, правило Крамера, метод Гаусса

Приближенное решение систем линейных алгебраических уравнений в Mathcad можно реализовать, например, с использованием функции Find, описанной в подразделе "Аналитические вычисления" главы "Mathcad. Общие сведения".